PID算法学习及循迹算法开发
前言
没想到还没接触积分和微分,最近的机械臂和小车就要用到PID算法了,距离比赛也没多久了,PID作为自动化控制基本绕不开的一个算法,没想到刚刚步入大一我就要为比赛详细学习了,着实有点怪怪的,不过看起来了解积分和微分的符号和计算方式,整个算法就一目了然了,下面是我学习的一个过程

废话不多说,开始PID算法的学习然后来攻克循迹算法
PID算法
首先看了一个b站网友的学习笔记,点击查看
PID算法未简化的公式是u(t) = Kₚ × e(t) + (1/Tᵢ) ∫ e(t) dt + Td × (de(t)/dt)
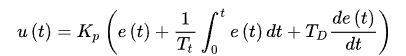
第一眼看呆了,这什么符号,看了下,说是一个比例项,积分项,微分项
究竟什么是积分什么是微分,当然积分高中就接触过了,但在大学有个符号积分符号∫ 和d 注意一下
知识补充
积分学

接下来还有个微分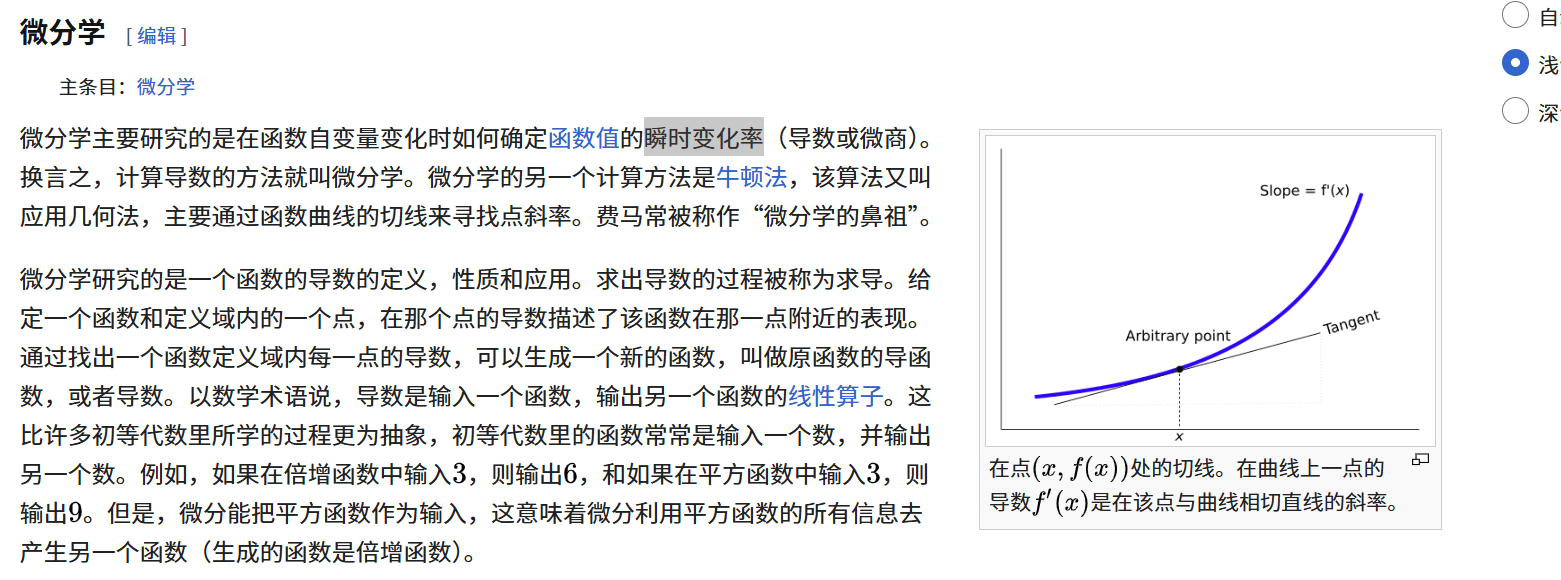
可以发现积分是追求无限小,而微分追求的是瞬时变化率极限,积分当然同样也是向着极限
莱布尼茨记号
通过简化可以利用dy/dx表示X2的导数2x
 回顾
回顾
在b站网友的教程中PID被取出需要自己经过实验数据来定义的系数,剩下部分和系数一起,积分∫ 可以理解成S(Sum求和)
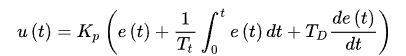
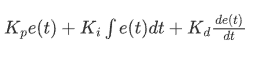
那我们来翻译这个公式,
P
e(t)是一个函数,得出来错误率的呈现函数图像,
I
e(t)图像中,时间0到t的错误部分累积之和
D
de(t)与dt的瞬时变化率
在无限循环下,D中的瞬时变化率会不断变化生成一次函数,实现未来预测
循迹算法
查看例程及官方原理讲解:点击前往
它原理通过线性回归得到切线再换算角度,小车跟着变化前进就可以了,这个变化是动态的存在误差需要PID算法纠正
本文是原创文章,采用 CC BY-NC-ND 4.0 协议,完整转载请注明来自 华灵社区
评论
匿名评论
隐私政策
你无需删除空行,直接评论以获取最佳展示效果

